Par Florent Gbongué, PhD*
Les pays de l’UEMOA ont élaboré des programmes nationaux de développement ambitieux, dans l’optique d’atteindre l’émergence dans un horizon donné[1]. Notons que la mise en place de ces programmes nécessite de mobiliser des ressources importantes, qui sont internes (recettes fiscales) ou externes (dettes). Dans cet article, nous nous intéressons à la mobilisation optimale des ressources externes à travers la détermination du coût optimal des emprunts sur le marché financier régional de l’UEMOA.
- Introduction
L’analyse des taux coupons sur les titres publics des pays de l’union révèle l’existence des écarts de taux implicites (ETI) ou primes de risque implicites, au regard de la structure par terme zéro coupon proposé dans les travaux de Gbongué et Planchet [2015f], Gbongué et al. [2017], Gbongué [2018a], Gbongué [2018b] et Gbongué [2019]. Notons que les ETI constituent, dans la théorie financière, une mesure essentielle de la perception du risque souverain implicite des investisseurs en monnaie locale. En pratique, ils comprennent deux composants, qui sont imputables au défaut et à la liquidité implicites des titres publics (cf. Stander [2005]).
La structure par terme des ETI peut être définie comme étant la fonction qui, à une date donnée, pour chaque maturité, indique la prime de risque implicite que l’émetteur souverain devrait s’acquitter. Par conséquent, elle participe à la détermination réelle du coût de financement des pays lorsqu’ils mobilisent des ressources sur le marché financier local (cf. Gbongué [2019]). Dans la littérature, l’existence d’une prime de risque sur les obligations d’Etat est justifiée par les travaux de Merrick [2001], Duffie et al. [2003], Vrugt [2010], Bernardo et Caio [2008], Berardi et al. [2004], etc., au regard du défaut de paiement de certains pays à l’échelle internationale.
En effet, Merrick [2001] propose un modèle capable de déterminer simultanément le taux de recouvrement RV et la structure par terme des probabilités de défaut en univers risque neutre pour la Russie et l’argentine. Ce modèle est appliqué sur les Eurobonds en dollar durant la crise de défaut de la Russie en 1998. Ainsi, les écarts de taux peuvent être déduits à partir de la relation de Duffie et Singleton [1999]. Dans le contexte du Brésil, Bernardo et Caio [2008] analyse la perception du risque souverain des investisseurs en proposant un modèle dynamique paramétrique (en l’absence d’opportunité d’arbitrage) pour déterminer le taux de recouvrement RV et la structure par terme des probabilités de défaut en se basant sur les travaux de Duffie et Singleton [1999]. Avec un taux d’erreur inférieur à 0,08 %, ils concluent que le modèle est adapté pour tarifier de nouvelles émissions.
Au regard de ce qui précède, nous montrons, de manière originale, l’existence d’une prime de risque souveraine implicite dans la zone UEMOA, grâce à une méthodologie capable de quantifier les ETI selon deux approches (directe et indirecte), à partir des émissions souveraines observées au 31/12/2017. En pratique, nous présentons les résultats des modèles proposés dans Gbongué [2019]. En outre, nous conseillons l’approche indirecte pour déterminer la prime de risque implicite exigée par les investisseurs car elle permet de la décomposer et de distinguer la part attribuable aux primes de crédit et de liquidité implicites.
- Méthodologie
Selon l’approche utilisée, l’estimation des ETI requiert en amont le calibrage d’un modèle de construction d’une courbe des taux zéro coupon (ZC), qui est une étape cruciale. En aval, nous supposons que le prix de l’obligation est risqué, ce qui nécessite une valorisation particulière de ce prix. Cette dernière fait ressortir un facteur de risque, dont son évaluation par le modèle de Nelson Siegel [1987], permet d’obtenir les ETI.
Toutefois, l’approche indirecte est un peu complexe car elle requiert plusieurs étapes. La première concerne le calibrage d’un modèle de construction d’une courbe des taux ZC. La seconde suppose l’existence d’un risque de défaut de crédit. Dans ce contexte, la valorisation du prix de l’obligation s’inspire du modèle de Merrick [2001] et les primes de crédit sont obtenues en utilisant le modèle de Gumbel.
Enfin, nous proposons une nouvelle valorisation du prix de l’obligation dans la dernière étape car nous supposons la présence simultanée des primes de crédit et de liquidité. Ayant déterminé les taux zéro coupons et les primes de crédit dans les deux premières étapes, nous calibrons le modèle de Weibull afin d’obtenir les primes de liquidité. La section 3 présente l’évolution de la structure par terme des taux ZC, ainsi que des écarts de taux de crédit et de liquidité.
- Illustration numérique
En appliquant les modèles décrits supra sur les données de la BRVM en circulation au 31/12/2017, nous obtenons en premier lieu la structure par terme zéro coupon, illustré par la figure 1 ci-dessous :
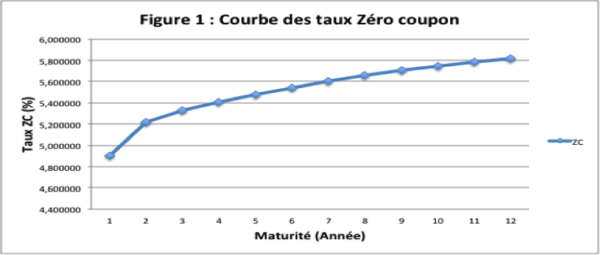
Cette courbe des taux ZC est croissante, de pente positive, ce qui est en accord avec le contexte économique actuel de l’union. Ce résultat est important car il permet d’obtenir des primes de crédit et de liquidité, qui reflètent la réalité économique de l’UEMOA. Elles sont naturellement croissantes sur les maturités observables (0 à 12 ans). La figure 2 illustre cette assertion :
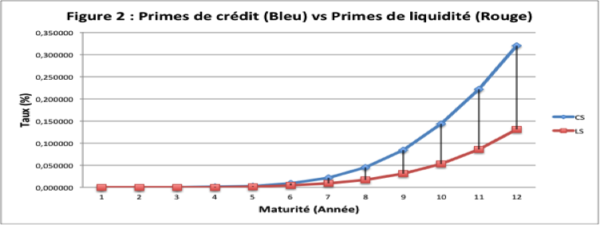
| Afin de légitimer la quantification des primes de crédit et de liquidité par la méthode indirecte, elle est comparée à la méthode directe. L’analyse comparative constate que les deux méthodes présentent des résultats quasiment similaires, comme l’illustre la figure 3 ci-dessous : |
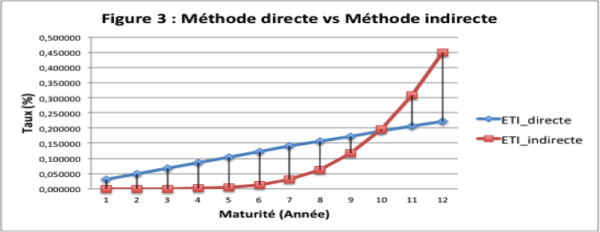
- Conclusion
Dans cette contribution, nous avons pu constater que son originalité vient, en premier lieu, dans sa capacité à démontrer l’existence d’une prime de risque souveraine implicite. En second lieu, il présente deux approches différentes (directe et indirecte) pour quantifier ces primes de risques implicites, qui aboutissent à des résultats similaires. Enfin, il permet de rendre observable les primes de crédit et de liquidité dans le contexte de la zone UEMOA, ce qui permettra de mieux structurer et piloter la dette publique. Si nous avons proposé la courbe des ETI de référence, en revanche, il est possible d’obtenir la courbe des taux de chaque pays de l’union, en appliquant un coefficient de choc à la courbe des ETI de référence, matérialisant le risque intrinsèque de ces pays.
[1] Par exemple, la Côte d’ivoire souhaite atteindre l’émergence en 2020.
* Florent Gbongué, docteur en Actuariat de l’université de Lyon. Spécialiste de l’économie et de la finance, il est auteur de plusieurs articles scientifiques et professionnels et intervient comme « reviewer » à la revue Africaine de Développement. Contact : +225 47 28 20 72/ florent.gbongue@gmail.com



